La fatica del salire

Quando ho manifestato ad una cara e paziente amica che stavo pensando di scrivere qualcosa su questo argomento ho visto che ha accennato un misterioso sorrisetto subito rientrato; allora mi sono detto che sì forse stavo per analizzare l’ovvio, ciò che tutti noi intuitivamente conosciamo e che normalmente non merita indagine.

Ma nel mio passato sono stato abituato, per motivi di lavoro, a chiedermi il perché delle cose anche se sono di una banale evidenza.

Allora su le maniche, raccogliamo un po’ di materiale sui libri, sul Web e ragioniamoci sopra.

Innanzitutto voglio fare una doverosa premessa: qui si semplifica tutto il possibile. Ci sono fior di professori, allenatori e sponsor pagati per analizzare tutto ciò che attiene alla esecuzione di un gesto sportivo, alla meccanica del corpo umano, alla efficienza del sistema cardiocircolatorio, alla responsabilità delle varie fibre muscolari che potrebbero farsi matte risate se tentassi di giocare sul loro terreno.

Mi limiterò invece ad usare poche reminescenze scolastiche di fisica per fare alcune considerazioni.

Camminare in pianura

Questa è una delle nostre prime conquiste da bambini; quando per la prima volta passiamo dal gattonare alla posizione eretta e ci avviamo ondeggiando facciamo emettere gridolini di giubilo e di apprensione a genitori, nonni e parenti tutti. Poi pian piano le nostre incertezze cessano e acquistiamo quella che sarà la “firma” della nostra camminata, ognuno diverso in qualcosa dall’altro. Però è un’attività che ci è abituale (o dovrebbe esserlo) e la svolgiamo quotidianamente a diverse velocità, dalla tranquilla passeggiata alla corsetta per prendere il treno.

Il movimento è semplice, automatico ed il lavoro che si fa per la fisica è 0. Proprio così! Il lavoro L è definito come prodotto tra una forza F necessaria a spostare un corpo e la lunghezza dello spostamento S. Occorre che la forza sia orientata nello stesso verso dello spostamento. Nella nostra camminata la forza in gioco è il nostro peso, diciamo 70 kg, ma è diretta perpendicolarmente al suolo che le oppone una reazione uguale e contraria annullandola. Quindi (sento già le proteste!) il lavoro effettuato è nullo.

Fortunatamente (o sfortunatamente) non è così: dobbiamo applicare una forza nella direzione del movimento per superare attriti, resistenze varie e per portare, ad ogni passo, la gamba posteriore a fianco e poi davanti a quella anteriore. Tutto ciò è stato misurato e quantificato dagli esperti per cui un tizio che pesi 70 kg che cammina alla velocità di 3 km/h per un’ora consuma ca. 210 kcal (chilocalorie) cui corrisponde un lavoro svolto di ca. 50 kJ (chiloJoule). Raddoppiando la velocità (6 km/h) il nostro eroe consumerà 378 kcal pari a ca. 83 kJ. Per la gioia delle signore dirò che nel primo caso si consumano 26 g di peso e nel secondo 47 g. In realtà esistono diversi siti che effettuano questi calcoli e…..non ce ne sono due che diano risultati uguali ma a noi, data la mia premessa,  interessa una valutazione qualitativa e non rigorosamente quantitativa delle cose. Immaginate, infatti, nella macchina uomo quali e quanti possono essere i fattori che influenzano la nostra camminata: la temperatura, l’umidità (afa), l’avere o non avere pranzato, la stanchezza, l’età, dolori articolari, crampi, noia, insomma è veramente difficile fare i “farmacisti” e valutare con precisione il dispendio calorico!

Correre in pianura

La camminata veloce si può trasformare in corsetta e poi in corsa vera e propria, anche queste apprese nei primi due anni della nostra vita, se lo slancio che imprimiamo al nostro corpo nella effettuazione del passo fa sì che il tempo di permanenza del piede sul terreno diminuisca considerevolmente. Mentre nella camminata più o meno veloce il passo viene svolto principalmente dal tallone e l’avampiede quasi non partecipa alla spinta, nella corsa si parla di “rullata” del tallone a terra e susseguente spinta in avanti impressa con l’avampiede. Il contributo dell’avampiede è tanto maggiore quanto lo è la velocità della corsa; basso nella corsetta “per la salute” o jogging e altissimo nelle corse in pista come i 100 m dove il tallone scompare e anche le scarpette specifiche hanno i chiodi solo nella parte anteriore dove la spinta viene esercitata. Anche qui ci vengono in soccorso i “guru” che quantificano in 750 kcal l’energia (o lavoro) speso per un uomo di 70 kg che corra per un’ora ad un ritmo blando di 6’/km ( i runner misurano così la loro velocità, in minuti per km) e in 1200 kcal l’energia spesa da un maratoneta di buon calibro che corre per un’ora a 3’30”/km. Anche qui i parametri in gioco sono come nel paragrafo precedente tanti e possono grandemente influenzare prestazioni e risultati. Tanto per fare un esempio, a 40 anni correvo una mezza maratona (21,097 km) al ritmo di 4’30”/km. Oggi sarei felice di farlo a 5’15”/km. Ma non solo l’età è condizionante, tutti i fattori già elencati lo sono, incluso l’umore e l’euforia piuttosto che la depressione. Non potremmo altrimenti parlare di giornate “no” e di giornate “sì”.

Camminare in salita (alias montagna)

Ed ora veniamo al titolo dell’articoletto. Perché dunque quando saliamo per i nostri amati monti la camminata che in pianura ci pesa relativamente si trasforma a volte in una fatica enorme, specialmente se protratta nel tempo? Il motivo sostanziale è che al dispendio energetico più o meno valutato per la camminata in piano dobbiamo aggiungere un nuovo contributo e per farlo dobbiamo ricorrere ad una delle cosiddette macchine semplici della fisica: il piano inclinato.

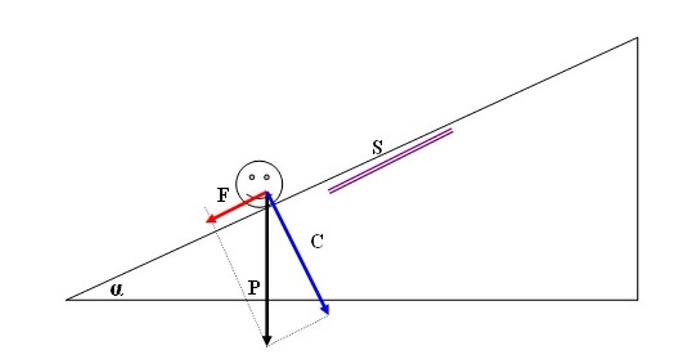
Il piano inclinato qui simula la nostra montagna; il nostro omino di peso P = 70 kg vuole salire su un pendio inclinato dell’angolo α rispetto all’orizzontale e ad ogni passo effettua un movimento pari ad S (es.60 cm). Una semplice regoletta detta “parallelogramma delle forze” che molti di voi ricorderanno permette di scomporre la forza peso P in due forze, l’una perpendicolare al pendio C e l’altra parallela al pendio F. Mentre C viene completamente annullata dalla reazione del terreno, che non può essere penetrato, la forza F, che tende a trascinarci in basso, è quella da vincere per effettuare lo spostamento S (un passo).

Se ne deduce che per salire il pendio, oltre alle energie già viste per la camminata in pianura, occorrerà somministrare una ulteriore energia pari al lavoro L = F * S

Raggranellando qualche nozione di trigonometria (odiosa!) si ricorda che F = P * sen α

Per fare un esmpio, se α  = 16.7° (gli corrisponde una pendenza del 30%) saranno:

F = 70 kg * sen 16.7° = 20.11 kg

Che è lo sforzo da fare ad ogni passo per salire il nostro pendio (non male no?)

A questo sforzo corrisponde un lavoro ad ogni passo pari a:

L = F * S = 20.11 kg * 0.6 m = 12.07 kgm (o meglio ancora 118.35 J o 28.29 calorie)

Non spaventatevi, qui si parla di “piccole calorie”. Senza tediarvi con calcoli, volendo estendere il lavoro al percorrere 5 km su un pendio costante  di pendenza 30% dovremo aggiungere 246 kcal a quanto speso per una equivalente camminata in pianura.

Teniamo comunque presente che tutto ciò si somma alle calorie spese per il metabolismo basale (il costo di essere vivo, respirare, digerire, ecc.) e a quanto speso per le normali attività leggere. Questa “tara” varia tra le 1500 e le 2500 kcal giornaliere.

Anche qui non si vuole fare i “farmacisti” ma semplicemente rendersi conto di cosa comporti aumentare o diminuire la pendenza della nostra salita. Infatti ad essere precisi occorrerebbe anche pensare che l’estensione del passo, originariamente posta di 60 cm, si accorcia anch’essa con la pendenza e con la fatica e quindi il numero di passi per una determinata distanza aumenta e con esso anche il lavoro da compiere.

Qui di seguito troverete una tabella che vi dà i vari parametri di cui abbiamo parlato in funzione della pendenza del terreno. Come si vede a parità di passo (che è una approssimazione) al variare della pendenza diminuisce la proiezione orizzontale del passo (avanzamento) e aumenta la proiezione verticale (DSL=dislivello) e aumenta anche lo sforzo che devo effettuare. Tralascio l’aspetto calorico che interessa più coloro che desiderano mantenere la linea e che esula dalle intenzioni del mio scritto.

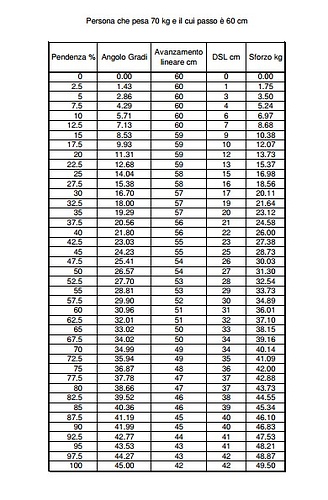
                                                                   (Visualizza PDF)

La pendenza è qui contenuta tra valori “ragionevoli” ossia tra il piano assoluto e una pendenza 100% (cui corrisponde un angolo di 45°). Oltre è inutile andare perché già superando pendenze dell’ordine del 50% si è al limite della quadrupedia e bisognerebbe spostare il ragionamento sull’arrampicata anziché sull’escursionismo.

Facciamo un po’ di statistica

Poiché non abbiamo strumenti matematici o altri esatti per fare deduzioni allora conviene collezionare un po’ di dati da esperienze fatte sul campo (cioè in montagna) per derivarne, se possibile, dei criteri che ci consentano di prevedere l’influenza della pendenza.

Ho raccolto per questo parecchi dati, qui sotto riportati, provenienti da mie gite significative in questo ambito. Li vedete rappresentati nella seguente tabella ma, ovviamente, ognuno di noi potrebbe costruire la sua personale tabella e probabilmente sarebbero diverse le une dalle altre….ma non troppo!

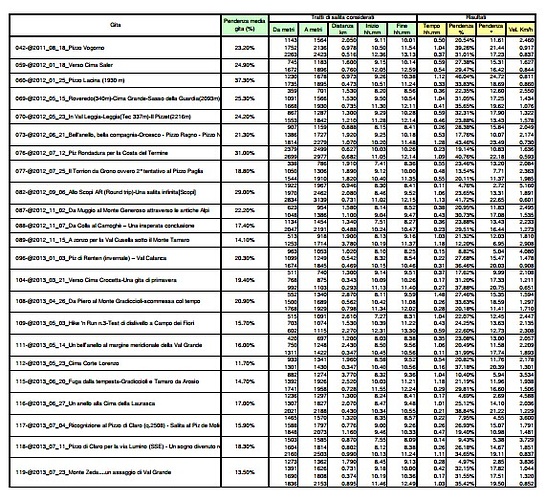
                                                              (Visualizza PDF)

Probabilmente la tabella sarà poco leggibile ma troverete nella relazione i file .PDF di tutte le tabelle per poterle meglio consultare. In sostanza la tabella raccoglie diverse gite e di ognuna considera due o più tratti in salita a pendenze diverse calcolando con quali velocità ho percorso ognuno dei tratti. Ribadisco che le distanze percorse cui si applicano le velocità misurate si riferiscono alla proiezione sul piano orizzontale delle distanze stesse come mostrerò più avanti.

Le conclusioni

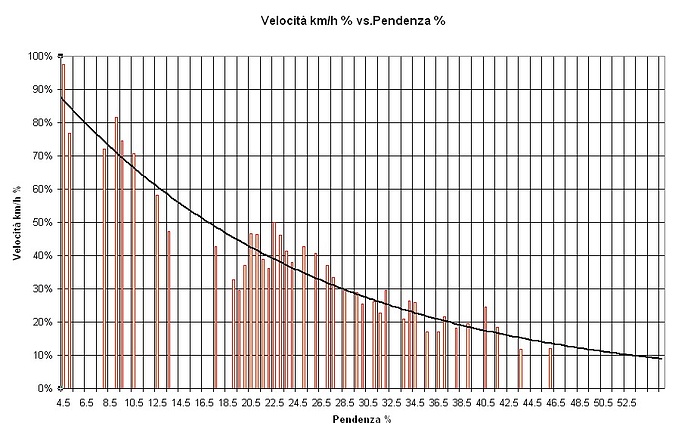
Si possono trarre conclusioni allora? Sembrerebbe di sì. Con un lavoro antipatico e certosino di cui vi risparmio anche la descrizione ho riportato su un grafico le velocità che vedete nella colonna più a destra della tabella precedente in funzione della pendenza % dei vari tratti (terza colonna da destra) ottenendo così un bel grafico difficile da capire se non intervenisse la linea di tendenza che copre un continuum di casi. In altre parole i dati utilizzati per costruire il grafico non sono tantissimi ma la linea di tendenza ci permette di sapere quale sarà la nostra velocità di percorrenza di una salita in ogni caso. Basterà sapere la pendenza % del tratto L ; individuare tramite la linea di tendenza quale sarà la velocità V che potremo tenere in km/h e con una semplice divisione derivare il tempo T che impiegheremo (attenzione: il tempo arriva in ore e centesimi; occorre convertire i centesimi in minuti primi).

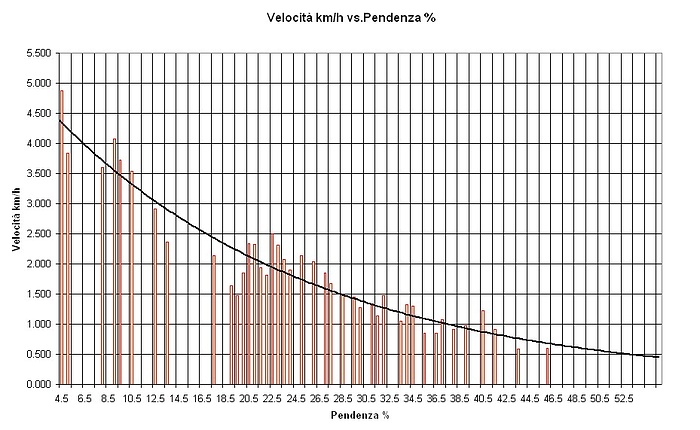
Funziona? Ho provato ad utilizzare questo strumentino in parecchi miei casi e con le dovute tolleranze dovute all’influenza di altri fenomeni, quelli che ci fanno dire “giornata sì” o “giornata no”, devo dire che funziona.

Vi chiederete: ma serve? Cosa me ne faccio? Dipende da voi, come sempre. Chi va in montagna senza fare troppe congetture mentali lo cestinerà immediatamente. Chi gradisce sapere il perché delle cose potrebbe ritenerlo di qualche interesse.

Un caso
Per meglio mostrare come si usa lo strumentino consideriamo il profilo di una mia recente gita.

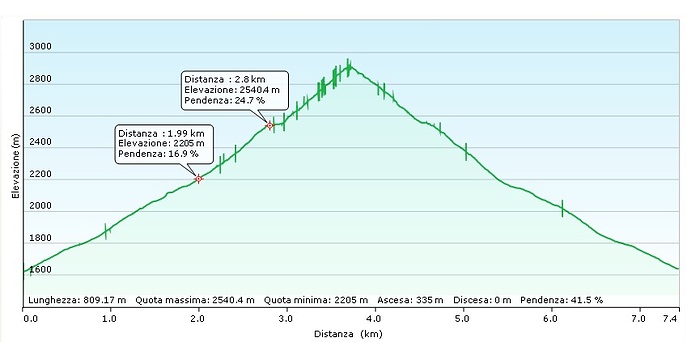
Come potete vedere ho isolato il tratto racchiuso tra i due fumetti. In basso potete vedere che la sua lunghezza è di ca. 810 m e che la sua pendenza è del 41.5%. Dal grafico precedente si capisce che la velocità ipotetica tenuta sarebbe di ca. 0.8 km/h.

In realtà sono transitato per il primo punto alle 9:52 e per il secondo punto alle 10:55. Ho quindi impiegato 1h03’ per percorrere il tratto. Applicando la regoletta T = L / V posso scrivere che il tempo dovrebbe essere T = 0.810 km / 0.8 km/h e cioè T = 1h00’ …….non male vero?

Generalizzazione
Poiché ognuno di noi ha parametri personali diversi ho ridisegnato il grafico della Velocità in funzione della Pendenza in forma totalmente percentuale in modo che chiunque possa applicarlo ai propri parametri personali.

                                                              (Visualizza PDF)

A questo punto…..buone salite!

gbal